Can the Graph of Y=f(X) Intersect a Horizontal Asymptote
Learning Outcomes
- Employ the caste of the numerator and denominator of a rational function to determine what kind of horizontal asymptote it will take.
- Calculate slant asymptotes.
- Decide the intercepts of a rational part in factored grade.
While vertical asymptotes describe the beliefs of a graph as the output gets very large or very pocket-sized, horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. Remember that a polynomial'southward end beliefs will mirror that of the leading term. Likewise, a rational part's end behavior will mirror that of the ratio of the leading terms of the numerator and denominator functions.
There are 3 distinct outcomes when checking for horizontal asymptotes:
Case 1: If the degree of the denominator > degree of the numerator, there is a horizontal asymptote at [latex]y=0[/latex].
Instance: [latex]f\left(x\right)=\dfrac{4x+2}{{10}^{2}+4x - 5}[/latex]
In this case the terminate behavior is [latex]f\left(x\right)\approx \frac{4x}{{x}^{two}}=\frac{iv}{ten}[/latex]. This tells us that, as the inputs increase or decrease without bound, this function will deport similarly to the function [latex]k\left(10\right)=\frac{4}{x}[/latex], and the outputs will approach aught, resulting in a horizontal asymptote at [latex]y=0[/latex]. Notation that this graph crosses the horizontal asymptote.
Horizontal Asymptote [latex]y=0[/latex] when [latex]f\left(x\right)=\dfrac{p\left(ten\right)}{q\left(10\right)},q\left(x\right)\ne{0}\text{ where degree of }p<\text{degree of q}[/latex].
Case 2: If the caste of the denominator < degree of the numerator by ane, we become a slant asymptote.
Example: [latex]f\left(ten\right)=\dfrac{iii{10}^{two}-2x+ane}{x - one}[/latex]
In this case the end behavior is [latex]f\left(x\correct)\approx \frac{3{x}^{ii}}{x}=3x[/latex]. This tells us that equally the inputs increase or subtract without spring, this role volition acquit similarly to the function [latex]g\left(x\right)=3x[/latex]. As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote. Yet, the graph of [latex]g\left(x\right)=3x[/latex] looks similar a diagonal line, and since [latex]f[/latex] will deport similarly to [latex]g[/latex], it will approach a line close to [latex]y=3x[/latex]. This line is a slant asymptote (Note: the graph of the function itself is just a "sketch" within the parameters of the asymptotes).
Slant Asymptote when [latex]f\left(ten\right)=\dfrac{p\left(x\correct)}{q\left(x\correct)},q\left(ten\right)\ne 0[/latex] where caste of [latex]p>\text{ degree of }q\text{ by }1[/latex].
To find the equation of the slant asymptote, divide [latex]\dfrac{3{x}^{2}-2x+one}{x - ane}[/latex]. The caliber is [latex]3x+one[/latex], and the balance is 2. The slant asymptote is the graph of the line [latex]g\left(x\right)=3x+i[/latex].
Case three: If the degree of the denominator = degree of the numerator, there is a horizontal asymptote at [latex]y=\frac{{a}_{n}}{{b}_{northward}}[/latex], where [latex]{a}_{n}[/latex] and [latex]{b}_{n}[/latex] are the leading coefficients of [latex]p\left(ten\right)[/latex] and [latex]q\left(x\correct)[/latex] for [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(ten\right)},q\left(10\right)\ne 0[/latex].
Case: [latex]f\left(x\right)=\dfrac{three{x}^{2}+2}{{ten}^{2}+4x - v}[/latex]
In this instance the end behavior is [latex]f\left(x\right)\approx \frac{3{x}^{ii}}{{x}^{2}}=iii[/latex]. This tells the states that as the inputs grow large, this function will behave like the function [latex]g\left(x\correct)=3[/latex], which is a horizontal line. Every bit [latex]10\to \pm \infty ,f\left(ten\correct)\to three[/latex], resulting in a horizontal asymptote at [latex]y=3[/latex]. Annotation that this graph crosses the horizontal asymptote.
Horizontal Asymptote when [latex]f\left(ten\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\correct)\ne 0\text{ where degree of }p=\text{degree of }q[/latex].
Observe that, while the graph of a rational function will never cross a vertical asymptote, the graph may or may non cross a horizontal or slant asymptote. Also, although the graph of a rational function may take many vertical asymptotes, the graph will accept at most one horizontal (or slant) asymptote.
It should be noted that, if the degree of the numerator is larger than the degree of the denominator past more than than one, the stop behavior of the graph will mimic the behavior of the reduced cease behavior fraction. For case, if we had the function
[latex]f\left(x\right)=\dfrac{three{x}^{5}-{x}^{2}}{x+3}[/latex]
with end behavior
[latex]f\left(x\right)\approx \dfrac{3{x}^{five}}{x}=three{x}^{4}[/latex],
the end beliefs of the graph would look similar to that of an even polynomial with a positive leading coefficient.
As [latex]x\to \pm \infty , f\left(x\right)\to \infty [/latex]
A Full general Notation: Horizontal Asymptotes of Rational Functions
The horizontal asymptote of a rational part can be determined by looking at the degrees of the numerator and denominator.
- Degree of numerator is less than degree of denominator: horizontal asymptote at
- [latex]y=0[/latex]
- Degree of numerator is greater than degree of denominator by one: no horizontal asymptote; slant asymptote.
- Caste of numerator is equal to degree of denominator: horizontal asymptote at ratio of leading coefficients.
Example: Identifying Horizontal and Slant Asymptotes
For the functions below, identify the horizontal or slant asymptote.
- [latex]g\left(x\right)=\dfrac{6{x}^{3}-10x}{2{ten}^{3}+five{10}^{2}}[/latex]
- [latex]h\left(x\right)=\dfrac{{ten}^{2}-4x+1}{ten+2}[/latex]
- [latex]thou\left(x\right)=\dfrac{{ten}^{2}+4x}{{x}^{iii}-8}[/latex]
Effort it
Scout this video to see more worked examples of determining which kind of horizontal asymptote a rational function will have.
Example: Identifying Horizontal Asymptotes
In the sugar concentration problem before, we created the equation [latex]C\left(t\right)=\dfrac{5+t}{100+10t}[/latex].
Find the horizontal asymptote and interpret it in context of the problem.
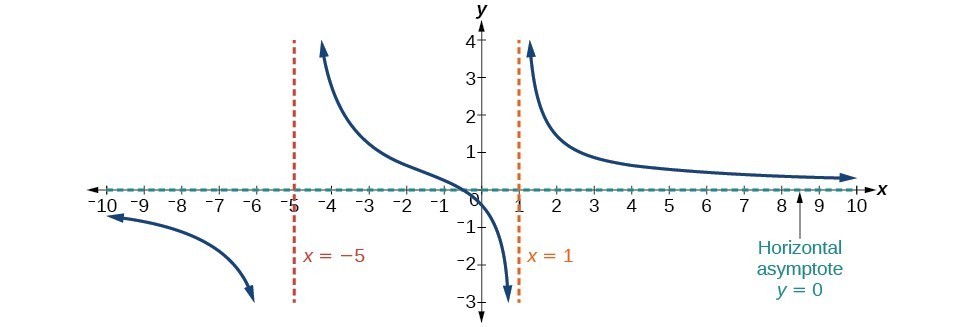
Example: Identifying Horizontal and Vertical Asymptotes
Find the horizontal and vertical asymptotes of the function
[latex]f\left(x\correct)=\dfrac{\left(x - 2\correct)\left(x+3\correct)}{\left(ten - 1\right)\left(x+2\right)\left(x - 5\right)}[/latex]
Try Information technology
Find the vertical and horizontal asymptotes of the function:
[latex]f\left(x\correct)=\dfrac{\left(2x - one\right)\left(2x+i\right)}{\left(x - 2\right)\left(x+3\right)}[/latex]
Prove Solution
Vertical asymptotes at [latex]x=two[/latex] and [latex]10=-three[/latex]; horizontal asymptote at [latex]y=4[/latex].
A General Note: Intercepts of Rational Functions
A rational function will have a y-intercept when the input is zero, if the function is defined at zero. A rational function volition not have a [latex]y[/latex]-intercept if the function is non defined at zilch.
Likewise, a rational role volition take [latex]x[/latex]-intercepts at the inputs that crusade the output to exist cipher. Since a fraction is only equal to zero when the numerator is zero, [latex]ten[/latex]-intercepts can merely occur when the numerator of the rational office is equal to nix.
Example: Finding the Intercepts of a Rational Function
Discover the intercepts of [latex]f\left(x\correct)=\dfrac{\left(ten - ii\right)\left(x+3\right)}{\left(10 - one\correct)\left(10+ii\right)\left(x - 5\right)}[/latex].
Try Information technology
Given the reciprocal squared role that is shifted right 3 units and down 4 units, write this as a rational part. Then, detect the [latex]10[/latex]– and [latex]y[/latex]-intercepts and the horizontal and vertical asymptotes.
Watch the following video to see more worked examples of finding asymptotes, intercepts and holes of rational functions.
Contribute!
Did you take an idea for improving this content? We'd beloved your input.
Improve this pageLearn More
Source: https://courses.lumenlearning.com/waymakercollegealgebra/chapter/horizontal-asymptotes-and-intercepts/
0 Response to "Can the Graph of Y=f(X) Intersect a Horizontal Asymptote"
Post a Comment